Εμβαδική ταχύτητα
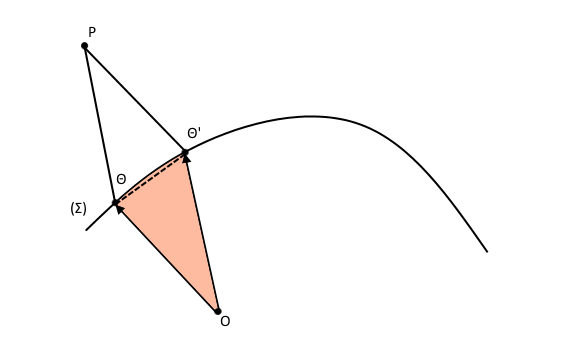
Στην Κλασσική μηχανική, η εμβαδική ταχύτητα (areal velocity, sectorial ή sector velocity) είναι ένα διανυσματικό μέγεθος που ισούται αριθμητικά με το μέτρο της ειδικής σχετικής γωνιακής ορμής του σώματος πολλαπλασιασμένο με 1/2. Εκφράζει πόσο γρήγορα διαγράφει ένα σώμα εμβαδόν (σύμφωνα με ένα σημείο αναφοράς Ο) όταν κινείται πάνω σε μία καμπύλη.Στο επόμενο σχήμα, θεωρήστε πως το υλικό σημείο (Σ) κινείται κατά μήκος της μαύρης καμπύλης. Θ και Θ' είναι δύο θέσεις που προσδιορίζονται από την διάνυσμα θέσης σύμφωνα με το Ο. Το εμβαδόν που διέγραψε το σώμα κατά την διάρκεια κίνησης του από το Θ στο Θ' είναι η χρωματισμένη περιοχή στο σχήμα. Η εμβαδική ταχύτητα ισούται αριθμητικά με αυτήν την διαγραμμένη περιοχή που εκτέλεσε σε χρονικό διάστημα Δt διαιρεμένη δια αυτό το χρονικό διάστημα στο όριο όπου το Δt << 1.
1]Προσέγγιση χωρίς συστήμα συντεταγμένων
επεξεργασίαΌπως αναφέραμε και παραπάνω, θεωρούμε υλικό σημείο που προσδιορίζεται από διανυσματική συνάρτηση r και κινείται στο xy επίπεδο. Έστω Θ και Θ' δύο θέσεις στην τροχιά του τις χρονικές στιγμές t και t + dt.
Το εμβαδόν που καλύπτει η ακτίνα r στο χρονικό διάστημα dt είναι ίσο κατά προσέγγιση με
Εάν θέσουμε r' = r + Δr
η σχέση γίνεται: Ισχύει όμως ό,τι Επομένως: Εαν διαιρέσουμε με και πάρουμε το όριο γίνεται:
και σε διανυσματική μορφή: Όπως παρατηρείται εύκολα, ο τύπος αυτός είναι ανεξάρτητος από σύστημα συντεταγμένων.
2]Καρτεσιανές συντεταγμένες
επεξεργασίαΣε καρτεσιανές συντεταγμένες συντεταγμένες έχουμε την διανυσματική συνάρτηση θέσης r.
και η ταχύτητα
Επομένως το εξωτερικό γινόμενο είναι: Έτσι γίνεται: Από όπου παίρνουμε:
Έτσι, η σχέση (1) γίνεται: και σε διανυσματική μορφή
3]Πολικές συντεταγμένες
Στις πολικές συντεταγμένες η διανυσματική συνάρτηση r είναι της μορφής και η ταχύτητα Οπότε: Χρησιμοποιώντας αυτήν την σχέση στην (1) έχουμε: και σε διανυσματική μορφή. Πηγές: "Θεωρητική Μηχανική, Τόμος Α', Νευτώνεια Μηχανική(τρίτη έκδοση)" , Ιωάννης Δ. Χατζηδημητρίου, Εκδόσεις Γιαχούδη Θεσσαλονίκη 2000
